Introduction

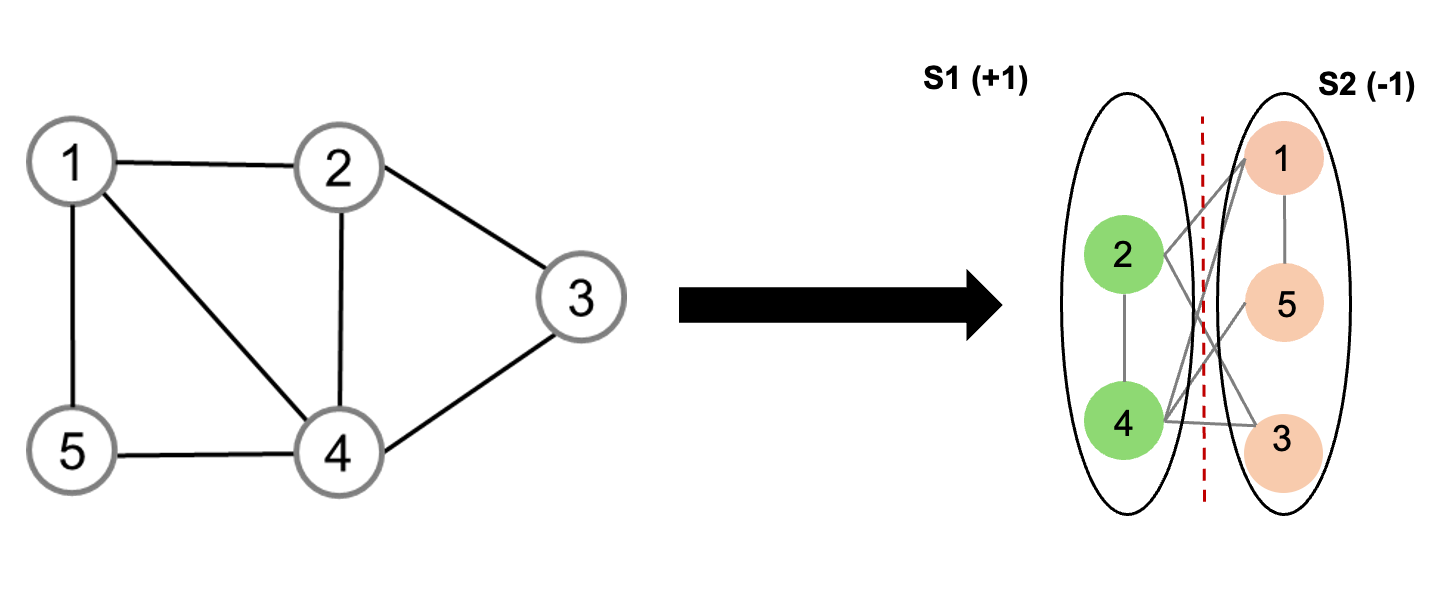
OmegaSync provides a service to compute the maximum cut (Max-Cut) of a graph.

The Max-Cut can be defined as:

\[ S^* = \arg \min_{S \in [1, -1]^N} H(S) \]

Where:

• \( S^* \in \mathbb{R}^N \) is the ground state of \( H(S) \)
• \( H(S) = -\frac{1}{2} S^T J S \)
• \( S \) is a spin vector, defined as \( S = [s_1, s_2, \dots, s_n] \)
• \( s_i \in \{1, -1\} \) represents the assignment of vertex \( i \) to one of the two sets (\( S_1, S_2 \)):
  • \( s_i = 1 \) if \( i \in S_1 \)
  • \( s_i = -1 \) if \( i \in S_2 \)
• \( J \) denotes the presence of an edge

OmegaSync integrates two computational methods

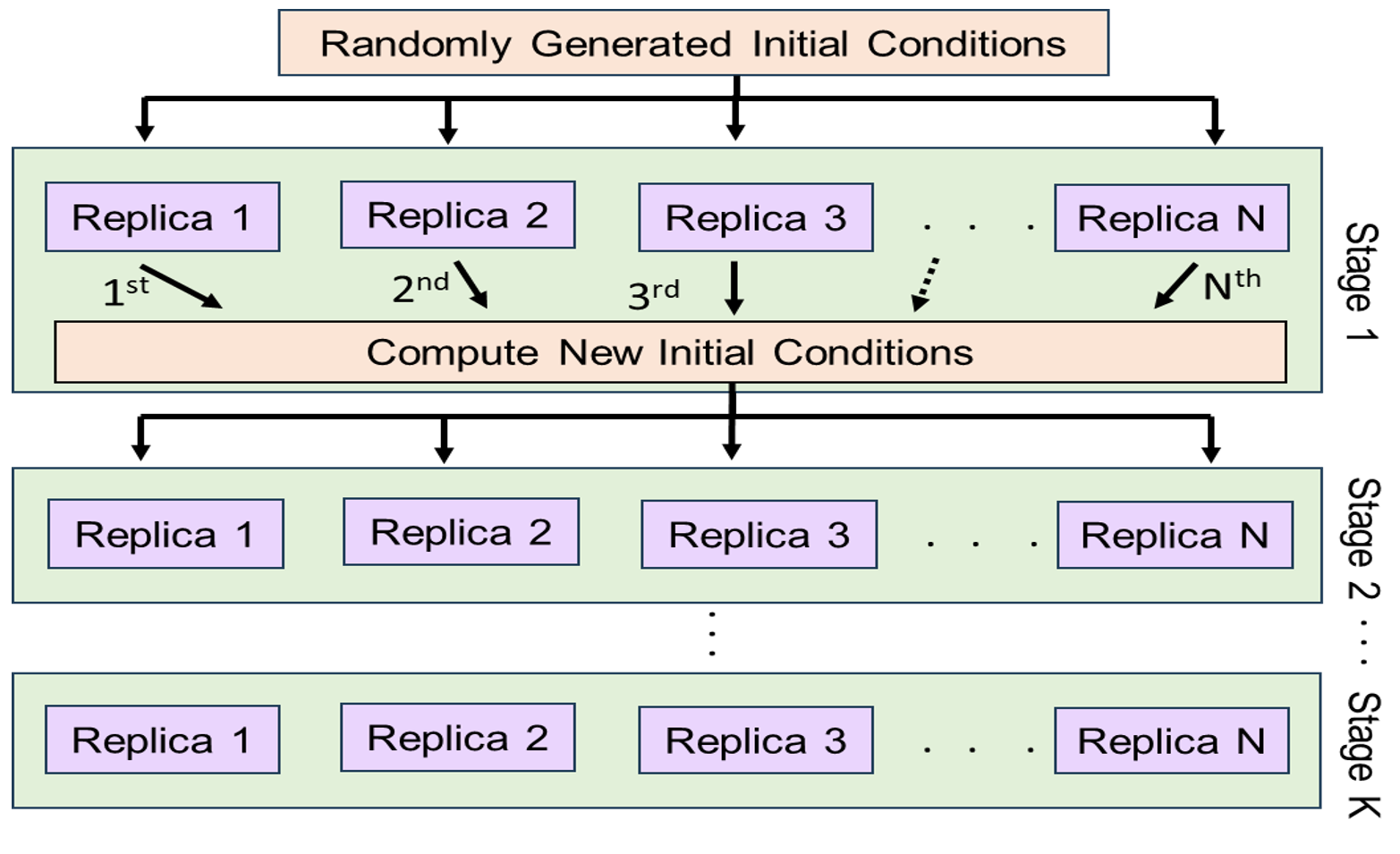
1. Population Annealing Monte Carlo (PAMC)

Population Annealing is a Markov Chain Monte Carlo variant that operates by simulating many independent solutions (or "replicas") in parallel, iterating through multiple stages to refine and converge toward the optimal solution [1].

2. Energy Minimization Inspired by Coupled Oscillators

A physics-inspired computational approach that maps optimization problems onto the dynamics of coupled oscillators, allowing for efficient exploration of the solution space. The continuous-time dynamics of the coupled oscillator system can be expressed mathematically as:

\[ \frac{d \phi_i}{dt} = -A_c \sum_{j=1, j \neq i}^N J_{ij} \sin(\phi_i(t) - \phi_j(t)) - A_s \sin(2\phi_i(t)) \]

Parameters that Govern Oscillator Behavior

The solver requires specific parameters as input to govern the behavior of the oscillators in the system. These parameters set the dynamics of the system and influence how the solver explores the solution space. Below is a description of the key parameters:

• A_s: Sets the strength of coupling from the sub-harmonic injection locking signal.
• A_c: Sets the strength of coupling between oscillators.
• tstop (Time Stop): Determines the total simulation time for the oscillator dynamics. Longer ‘tstop’ values allow the solver to perform more iterations, providing greater opportunities to refine solutions but at the cost of increased computation time.

Resource Parameters

In addition to the oscillator dynamics, the solver requires parameters that define the computational resources and the granularity of the solution search.

• Replica:
  • Definition: Specifies the number of independent solver runs for the given problem.
  • Role: Each replica starts from a different initial configuration, ensuring broader exploration of the solution space. More trials increase the probability of finding the global optimum. Note that the increase in the number of replicas will increase the computational resources used along with the time-to-compute. For this version, we set it by default to 512.

Input File Format

Example Format (what the .txt file should include):

4 4 5
2 1 1
3 1 1
3 2 1
4 2 1
4 3 1
      

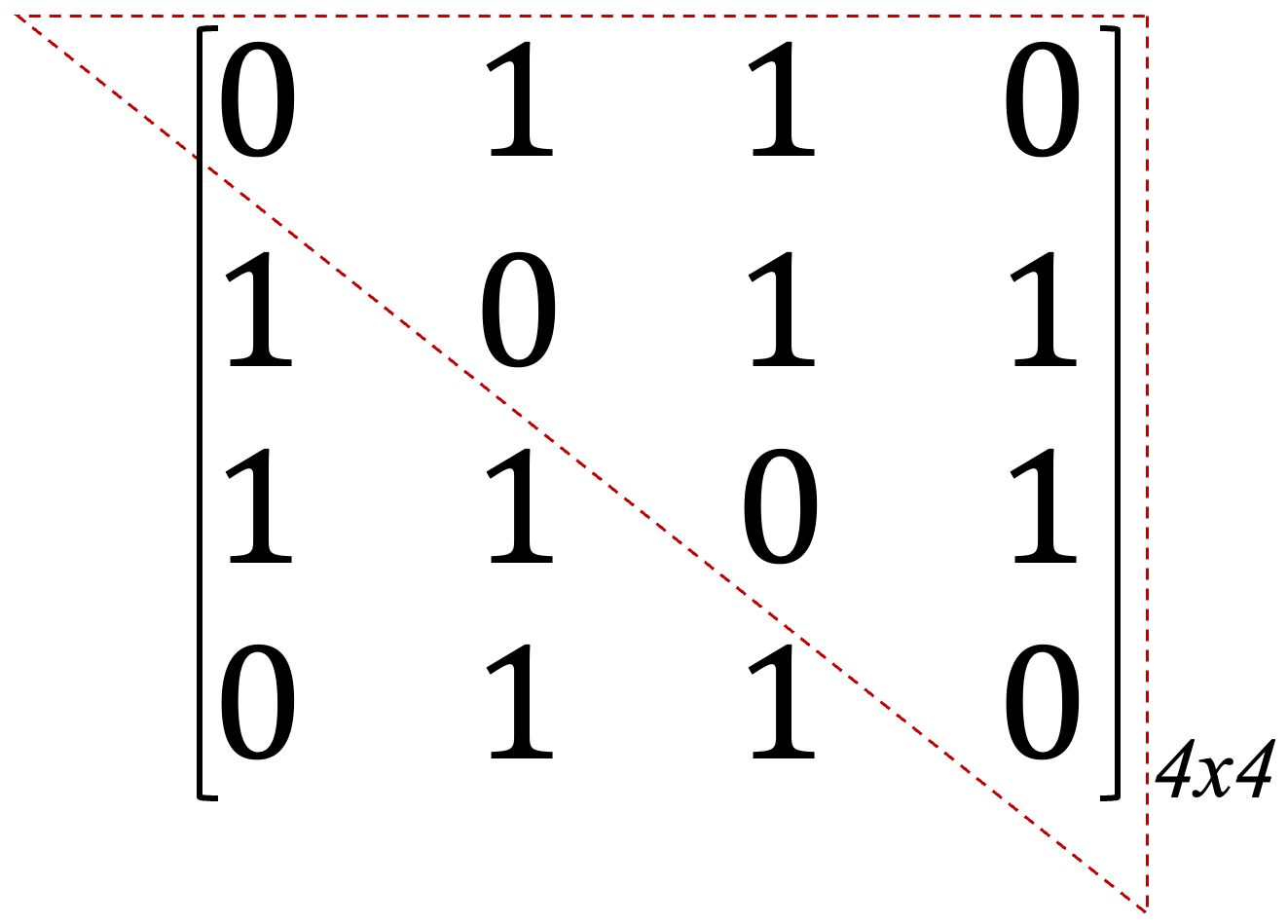
Matrix Size and Number of Entries

The first line specifies the matrix dimensions and the number of non-zero entries: Example: 4 4 5 means the matrix has 4 rows and 4 columns with 5 non-zero entries on the upper half matrix. Make sure the matrix is symmetrical in nature.

Data Lines

Each subsequent line represents a non-zero entry in the format: i j value, where i is a row number, j is a column number, and value is a non-zero edge weight. The equivalent matrix corresponding to the example is shown below:

Please refer to MTX Matrix Market Format for further information.

Instructions for Uploading the Input File

• Upload a Valid .txt File: Make sure the input file is described in an edge list format as mentioned above.
• Graph Validation Process:
  • Matrix Size: The first line of the file must specify the number of nodes and edges accurately. Any mismatch between the declared values and actual data will result in an error.
  • Non-Zero Weights: Edges with zero weight are invalid and will trigger a validation error.
  • Duplicate Edges: Edges between the same pair of nodes with identical weights should appear only once in the file.
  • Undirected Graph Format: For undirected graphs, an edge like (1, 2) should not also appear as (2, 1).
  • Self-Loops: Edges where both endpoints are the same (e.g., 1 1 3) are generally invalid unless specifically required.
  • Valid Data Types: All node identifiers and edge weights must be numeric.
• Submission and Job Queueing: Once your file passes the validation check, you can proceed to submit your task. Upon submission, your job will be queued for processing.
• Email Notification: Once the job is completed, you will receive an email with the output and solution.

References

[1] Wang, W., Machta, J., & Katzgraber, H. G. (2015). Population annealing: Theory and application in spin glasses. Physical Review E, 92(6), 063307.